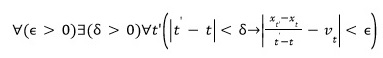Henrik Villanen

Mitä on kappaleen nopeus? Miten näkemystä kappaleen nopeudesta voidaan arvioida? Mekaniikassa kappaleen nopeudella on tärkeä rooli. Kun tarkastellaan kappaleita tai systeemejä, joissa kappaleet vaikuttavat toistensa paikkaan on hyvin tavallista tarkastella liikettä, vähintään implisiittisesti, nopeuden avulla. Mitä kappaleen nopeus ilmaisee? Kappaleen eteneminen aiheutti päänvaivaa metafysiikassa jo antiikissa. Tuolloin esitettiin erilaisia liikkeeseen liikkeen paradokseja, joiden oli tarkoitus osoittaa liikkeen mahdottomuus. Tällaiset paradoksit, kuten Zenonin paradoksi lähtevät purkautumaan, kun liikettä mallinnetaan asianmukaisesti matemaattisella välineistöllä, kuten mekaniikassa tehdään. Sen sijaan mallintamisessa käytettävien suureiden, kuten paikan, ajan, nopeuden ja muutoksen väliset yhteydet saattavat herättää kysymyksen siitä, mitä varsinaisesti ilmaistaan, kun kappaleen liikettä mallinnetaan näiden suureiden avulla. Voiko esimerkiksi kappaleella olla hetkellistä nopeutta (nopeutta tietyllä yksittäisellä ajanhetkellä), vai onko kappaleen nopeus riippuvainen sen kulkeman radan paikoista? Vai onko nopeus riippumaton suureista, joiden avulla kappaleen nopeus voidaan määrittää? Se, mitä erilaiset fysikaaliset suureet varsinaisesti tavoittavat tai ovat tavoittamatta liikkeeseen liittyvästä nopeudesta, ei välttämättä aukea kovinkaan helposti, vaikka käyttämällä erilaisia puhtaan matemaattisia menetelmiä voidaankin helposti esittää kappaleen liikettä määrittämällä sen nopeus tai esittämällä nopeuteen liittyviä tekijöitä.

Kappaleen nopeuden metafysiikan metodologiasta

Kappaleen nopeuden metafysiikan kysymyksiä voidaan lähestyä kahdella tavalla: käsitteitä luomalla tai niitä poissulkemalla. Esitän, että kappaleen nopeuden metafyysisissä kysymyksissä tulisi soveltaa eräänlaista luomis-poissulku-taktiikkaa, jossa sovelletaan järjestyksessä vuorostaan näitä molempia lähestymistapoja. Yhtäältä luodaan (voitaisiin myös sanoa konstruoidaan tai määritetään) mahdollisia kappaleen nopeuden käsitteen tulkintaa helpottavia metafyysisiä määritelmiä fysiikan harjoittamisessa käytetyn kappaleen nopeuden käsitteen perusteella. Tällöin kappaleen nopeuden metafyysiset tulkinnat voidaan nähdä jatkumona, eikä erillisenä tai itsenäisenä tulkinnallisena lisänä fysiikan näkemykselle kappaleen nopeudesta.

Toisaalta taas voidaan kehittää erilaisia kriittisiä ajatuskokeita, joilla pyritään poissulkemaan nopeuden metafyysinen määritelmä esittämällä tilanne, jossa luotu kappaleen nopeuden metafyysinen määritelmä täyttyy, mutta nopeuden käsitteen esiteoreettisen ymmärryksen perusteella kappaleella ei ole nopeutta tai nopeuden käsitteen teoreettisesti hedelmällisiä etuja.^[1]

Fysiikassa on standardi tapa määritellä kappaleen nopeus, ja tästä määritelmästä voidaan muodostaa kappaleen nopeuden määrittämisen mielekkyyden sekä soveltumisen ehdot. Näitä ehtoja voitaisiin kutsua kappaleen nopeuden sisäisiksi kriteereiksi: ne kuuluvat kappaleen nopeudelle kappaleen nopeuden sisäisen luonteen perusteella. 

Kappaleen nopeudella on kuitenkin myös tärkeä rooli fysiikan harjoittamisessa ylipäätään. Kappaleen nopeudella on hedelmällinen rooli liikkeen analyysissä mekaniikan yhtenä tärkeänä tarkastelun puolena. Nopeuden metafyysisen käsitteen arvioinnin kriteerinä tulee olla myös se, mitä fysiikan tutkiman maailman struktuurista voidaan sen avulla sanoa

.Jos metafyysinen nopeuden käsitys

i) täyttää kappaleen nopeuteen liittyvät sisäiset kriteerit, eli on yhteensopiva fysiikassa käytettävän määritelmän kanssa 

ja

ii) kestää testaamisen ajatuskokeilla,

niin tämä on peruste hyväksyä näkemys kilpailevista näkemysvaihtoehdoista.

Näen tämän strategian olevan mahdollinen kahdesta syystä: Yhtäältä siksi, että kappaleen nopeuden metafyysinen käsitys ei ole puhtaan tekninen, vaan myös esiteoreettisesti merkitsevä: jolloin voimme vertailla ajatuskokeissa  kappaleen nopeuden eri metafyysisiä määritelmiä määrittävien tekijöiden suhteiden paikkansapitävyyttä esiteoreettisen intuition avulla. Toisaalta siksi, että kappaleen nopeuden käsite on ylipäänsä hedelmällinen liikkeen analyysissä, mikä takaa perustan kappaleen nopeuden metafyysisen määrittämisen mielekkyydelle. Tarkoitukseni on näistä lähtökohdista puolustaa sellaista metafyysistä kantaa, jossa kappaleen nopeus samaistetaan kappaleen paikan-ajan–funktiona funktion ensimmäiseksi derivaataksi.

On oleellista, että tämä näkemys ei saa olla ristiriidassa kappaleen nopeuden määrittämiselle fysiikassa tai olla sen valossa epäuskottava. Tässä mielessä kappaleen liikettä käsittelevän liikkeen kehittyessä tulee aina miettiä, onko metafyysinen kappaleen nopeuden määritelmä uskottava nykyisten kappaleen liikettä käsittelevien fysiikan teorioiden valossa. 

Tässä tekstissä rajoitutaan käsittelemään nopeutta klassisessa mekaniikassa, jolloin jokaisessa tarkasteltavassa tilanteessa saatetaan tietää täsmällisesti onko tarkasteltava kappale paikallaan vai liikkeessä. Käsittelen tässä yhteydessä vain klassista, absoluuttista nopeutta ja rajaan tarkastelun ulkopuolelle esimerkiksi yleisen suhteellisuusteorian mukaiset nopeuskäsitykset.^[2]

Reduktionistinen käsitys kappaleen nopeudesta

Voimme ottaa lähtökohdaksi näkemyksen, että fysiikassa kappaleen nopeus voidaan määrittää kappaleen paikan muutoksena ajan kuluessa. Suoraviivaisinta on tämän perusteella tehdä metafyysinen johtopäätös: kappaleen nopeus on samaistettavissa sen kykyyn muuttaa paikkaa jossakin ajassa.

Tässä tarkastelussa ei oteta kantaa siihen miten tämä kyky pitäisi metafyysisesti ymmärtää, esimerkiksi dispositionaalisena ominaisuutena tai kulkuprosessin etenemiseen sisältyvänä puolena, jne. Kappaleen liikettä mallinnetaan kuitenkin esittämällä kappaleen paikka ajan funktiona, jolloin funktion ensimmäinen derivaatta antaa nopeuden lukuarvon matemaattisessa mallissa. Kappaleen nopeuden matemaattiselle mallille on varsin suoraviivaista antaa helposti ymmärrettävä geometrinen tulkinta, jonka esittelemme myöhemmin.

Antamamme metafyysinen tulkinta kuitenkin edellyttää, että kappale liikkuu välttämättä, jos sen paikka muuttuu (derivoituvaa rataa pitkin, jos kappaleella on nopeus) jossain ajan kestossa ^[3]. Kutsutaan tätä kappaleen nopeuden reduktionistiseksi metafyysiseksi käsitykseksi (myöhemmin selviää mistä nimitys tulee). Määritelmän mukaan kappaleella voi olla myös hetkellinen nopeus, joka voidaan määrittää kappaleelle vaikka aikaa ei kuluisikaan. Tämä hetkellinen nopeus määritetään ajan suhteen kappaleen paikan muutoksen raja-arvona, kun ajan kesto lähestyy nollaa ^[4]. 

On intuitiivista mallintaa kappaleen nopeutta funktion x(t) avulla, joka liittää tiettyyn ajanhetkeen t sen paikan x jossa kappale kyseisellä ajanhetkellä (t) kulkee. Voisi ajatella, että kappaleen keskinopeuden määrittäminen kappaleen kulkeman paikan muutoksen ja tarkasteltavan aikavälin suhteeksi on siten lähtökohdiltaan selvä. Mitä vähemmän kappale on siirtynyt tietyssä ajan kestossa, sitä pienempi kappaleen keskinopeus on ollut, ja mitä enemmän kappale on siirtynyt tietyssä ajan kestossa, sitä suurempi kappaleen keskinopeus on ollut. On kuitenkin selvää, että yleensä kappaleen nopeudella on mahdollista olla hetkellisiä vaihteluja tarkasteltuna aikana. Näin ollen pienentämällä kuljetun ajan aikaväliä aivan hetkelliseksi (ja siis myös kuljettua matkaa välittömyydessä kuljetuksi matkaksi) keskinopeus lähestyy tällöin hetkellistä nopeutta.

Alla on esitetty kuvaajien avulla havainnollistaen pääidea sille, miten raja-arvon avulla voidaan määrittää kappaleen hetkellinen nopeus tai se, että kappaleella ei ole hetkellistä nopeutta.

Alla on esitetty kuvaajien avulla tämän ajatuksen matemaattisen mallintamisen pääidea. Kun kappaleen liikettä kuvaavaa funktiota tarkastellaan yllä esitetyllä tavalla visuaalisesti paikka ajan muuttujana koordinaatistossa, niin voidaan kappaleen keskinopeus samaistaa intuitiivisesti funktion käyrän kulmakertoimeen ja hetkellinen nopeus derivaattaan, joka on tavanomaista yhdistää funktion tangenttiin tietyssä funktion käyrän pisteessä.

Tämän visuaalisen tulkinnan avulla on helppo esittää sekä reduktionistinen ajan metafyysinen näkemys, että sitä kritisoivien ajatuskokeiden pääidea.Toistaiseksi aion vain väittää, että tällainen reduktionistinen tulkinta kappaleen nopeudesta on mahdollinen sen perusteella, miten kappaleen nopeus määritellään fysiikassa. Uskonkin, että olen pystynyt esittämään sen varsin selkeästi ja ymmärrettävästi sekä havainnollistamaan tämän näkemyksen pääideaa visualisoinneilla riittävän hyvin. Nyt tarkastelemamme nopeuden määritelmä on reduktionistinen siinä mielessä, että nopeus redusoituu kappaleen kulkemaan rataan tietyssä ajassa. Tätä seikkaa ilmentää matemaattisessa mallintamisessa se, että kappaleen nopeus on aina suhteessa kappaleen kulkeman reitin pituuteen, joka saadaan kappaleen nopeusfunktiosta derivaatan käänteisoperaation eli integraalin avulla. Erityisesti kappaleella saattaa tämän näkemyksen mukaan olla hetkellinen nopeus, joka täsmällisesti palautuu kappaleen kulkemaan rataan nollaa lähestyvällä aikavälillä. Voimme esittää, että kappaleen hetkellinen nopeus (sikäli kuin sellainen kappaleella on) v_t täyttää siis seuraavan ehdon^[5]:

Tätä vastaan ei-reduktionistiset selitykset pitävät kappaleen nopeutta erillisenä niistä paikoista, joissa se radallaan on. Reduktionistista käsitystä voi kritisoida ainakin kahdella tavalla.

1. esittämällä tilanteen, jossa intuitiivisesti kappaleella on nopeus tietyllä hetkellä, vaikka kappaleen paikka ajan funktiona funktio ei olisi derivoituvissa tässä pisteessä tai
2. osoittamalla, että kappaleella on tietyllä aikavälillä derivoituva paikka ajan funktiona funktio, mutta nopeudella ei saavuteta sen hedelmällisyyttä liikkeen analyysissä (esimerkiksi kappaleen myöhempien paikkojen määrittämisen ominaisuutta).

Tarkastellaan seuraavaksi, kuinka reduktionistinen nopeuden määritelmä selviää eräistä näiden tyyppisistä kritiikeistä.

Määritelmän koettelu kriittisten ajatuskokeiden valossa

Seuraten John Carrollia ^[6] oletetaan, että kappale kulkee avaruudessa muuttaen paikkaa vakionopeudella, kunnes ajan hetkellä t₀ se katoaa. Ennen ajanhetkeä t₀ kappaleella on määritelmän mukaan nopeus, mutta hetkellä t₀ sillä ei ole nopeutta reduktionistisen nopeuden määritelmämme mukaan, sillä kappaleen paikkafunktiolla ei ole derivaattaa ajanhetkellä t₀. Tätä voi havainnollistaa sillä, että kappaleella nähdään olevan nopeus, kun kappaleen paikan muutosta ajan suhteen tarkastellaan lähestyessä hetkeä t₀ sitä edeltävästä ajasta, mutta entä jos tarkastelemme kappaleen liikkeen muutosta lähestymällä hetken t₀ jälkeisestä ajasta? Tätä on havainnollistettu alla olevalla kuvaajalla.

Vaikka tuntuu ilmeiseltä, että kappaleella on nopeus lähestyttäessä sen katoamishetkeä, tuleeko meidän sanoa yhtä lailla, että kappaleella on nopeus, kun lähestytään hetkeä t₀ tulevaisuudesta siten, että kappale syntyy maailmaan, vaikka sen rata ei olekaan derivoituva sillä ajanhetkellä, jolloin se syntyy maailmaan? Carrollin keskeinen väite on, että reduktionistinen nopeuden määritelmä tulisi hylätä, sillä se epäonnistuu tällaisissa tilanteissa analysoimaan kappaleen nopeutta mielekkäällä tavalla. Jos kappaleella on tietty hetkellisen nopeuden kuvaus kappaleen liikettä esittäessä, niin eikö tämän perusteella pitäisi pystyä sanomaan, missä paikassa se on tai tulee olemaan tietyn ajan päästä?

Pitäisikö tämän tai vastaavanlaisten esimerkkien, joissa kappaleen paikka ajan funktiona ei ole derivoituva, perusteella sanoa, että nopeuden käsite on loogisesti (mutta ei välttämättä nomologisesti) riippumaton kappaleen paikkojen tietyllä ajanhetkellä määrittämän radan suhteen ja näin ollen, että kappaleen liikettä ei tulisi samaistaa sen paikkafunktion derivaattaan ajan suhteen? Onhan olemassa kuviteltavissa oleva mahdollinen maailma, jossa Carrollin ajatuskokeen tilanne voi tapahtua. Mutta onko tämä oikeastaan varsinaisesti ongelma kappaleen nopeuden määritelmäämme vastaan? Miksi ei voida vain sanoa, että kappaleella ei ole hetkellistä nopeutta ajanhetkellä t₀, vaikka sillä voitaisiin nähdä olevan nopeus lähestyessä aiemmista hetkistä hetkeä t₀? Voidaan väittää, että Carrollin vasta-argumentti ei onnistu olemaan argumentti reduktionistista nopeuden määritelmää vastaan, sillä se ei osoita, että olisi tilanne, jossa nopeus olisi eri kuin minkä reduktionistinen nopeuden määritelmä antaa, koska molemmat hyväksyvät menneisyydestä päin määritettävän raja-arvon samaksi. Reduktionisti voi nimittäin vain todeta, että hänen määritelmänsä analysoi tilanteen siten, että kappaleella ei ole nopeutta ajan hetkellä t₀. Edelleen mielestäni Carrollin esittämän nopeuden avulla kappaleen paikan ennustaminen tietyn ajan päästä oikeammin säilytetään niin hyvin kuin on mahdollista. Kappaleen paikka nimittäin voidaan aina kun se on mahdollista määrittää tietyn ajan päästä kun lisäksi tietyt mekaniikan säilymisperiaatteet tunnetaan. Mielestäni ei ole lainkaan häiritsevää, että kappaleen paikkaa ei tiedetä heti siitä alkaen kun se on kadonnut liikkeen kuvaamisen kannalta määrittelemättömäksi. Itse asiassa kappaleen paikka voitaisiin hypoteettisesti määrittää mekaniikassa muiden tekijöiden, kuten siihen vaikuttavien voimien avulla, kuten esimerkiksi n-kappaleen tapauksissa tehdään kun lisäksi tietyt säilymisperiaatteet pätevät (esim. energian säilyminen ja liikemäärän säilyminen kun tehdään siirtymiä ajassa tai paikassa).

Toisaalta voimme Michael Tooleyn (1988) tarkastelusta inspiroituneena luoda vastaavanlaisen tarkasteltavan tilanteen^[7], jossa meillä on ohjelmaa näyttävä televisio, ja television näytön yksittäisiin pisteisiin tulee “televisio-ohjelmassa” yksi kerrallaan valo täysin satunnaisesti, mutta tietyn ajan, t₁-t₂, valo tulee puhtaalta sattumalta radalle, joka on derivoituva. Lisäksi oletetaan, että television näytöllä kulkee teleporttaava kärpänen rataa, jonka rata sattumalta on sama kuin ohjelman määrittämät pisteet television näytöllä. Tällaisen täysin avaruudessa satunnaisesti ”kulkevan” kärpäsen rata ”pomppii” tai ehkä oikeammin teleporttaa epäjatkuvasti avaruudessa paitsi aikavälillä (t₁-t₂), jolloin sen kulkema rata on sattumalta derivoituva (ja näin ollen jatkuva, jolloin on oletettava ääreton määrä pistemäisiä pikseleitä). Onko kärpäsellä nopeutta, kun se kulkee ajanhetkellä (t₁– t₂)?

Tätä saatetaan seuraten Tooleyta epäillä, koska kärpäsen nopeus ei missään määrin määritä sitä, missä paikassa se tulee olemaan jonkin ajan kuluttua, mikä saatetaan nähdä keskeiseksi nopeuden käsitteen hedelmällisyyden kannalta. Ehkä voidaan väittää jopa vahvemmin, että reduktionistisen nopeuden määritelmän mukaisella kärpäsen nopeudella ei ajatuskokeen tilanteessa ole selityksellistä roolia, mikä voidaan nähdä syynä olla postuloimatta ajatuskokeen tilanteessa lainkaan nopeutta, vaikka reduktionistisen nopeuden määritelmän mukaan kärpäsellä tulisi ajatuskokeen tilanteessa olla nopeus. Tämä ajatus kuitenkin olettaa, että hyväksyttäessä määritelmä, nopeuden postuloinnin lisäksi meidän tulisi pystyä postuloimaan kärpäsen tuleva paikka nopeuden perusteella, mikä ei ole alkuunkaan reduktionistisen kantamme mukainen ajatus. Ajatuskoe siis epäonnistuu olemaan vastaesimerkki reduktionistiselle nopeuden määritelmällemme. Nopeuteen yritetään tällaisissa ajatuskokeissa sisällyttää sellaisia asioita, jotka eivät siihen kuulu, mutta jotka voidaan tavanomaisesti nopeuden avulla liikettä tarkastellessa olettaa, kuten energian, pyörimismäärän ja liikemäärän säilyminen, joiden pätemistä teleportaatiotilanteessa on vaikea pystyä yhteensovittamaan ilman mitään lisästruktuurilla mallinnettavaa rakennetta.

Huomionarvoista on, että reduktionistinen kappaleen nopeuden määritelmä ei selviä kriittisten ajatuskokeiden koettelusta siksi, että vaikka ajatuskokeiden tilanteet ovatkin mahdollisia jossain metafyysisesti mahdollisessa maailmassa, niin tarkastelemamme reduktionistinen nopeuden määritelmä selviäisi kriittisistä ajatuskokeista johtuen muista maailman luonnonlaeista, joiden mukaan kappaleiden radat ovat aina derivoituvia ja että siksi nopeus ”sattuisi” selviytymään näistä kriittisistä ajatuskokeista. Tässä mielessä tarkastelemaamme reduktionistista kappaleen nopeuden määritelmää voidaan käyttää erilaisten kappaleen liikettä käsittelevien tilanteiden analyysissä itsenäisesti. Nämä syyt toimivat yhdessä evidenssinä sen puolesta, että kappaleen liikkeen reduktionistinen määritelmä toimii hyvänä kappaleen liikkeen metafyysisenä määritelmänä.

Lopuksi

Jos kappaleen nopeuden metafyysistä käsitystä lähdetään tarkastelemaan mekaniikan tavanomaisen määritelmän perusteella, niin reduktionistinen käsitys tarjoutuu kuin itsestään ja tavanomainen tapa mallintaa nopeutta tavanomaisella kappaleen liikkeen matemaattisella mallilla tekee reduktionistisen näkemyksen selkeästi ymmärrettäväksi. Kriittisillä ajatuskokeilla reduktionistista näkemystä voidaan koetella sen sisäisestä seikasta: nopeuden määrittämisestä oikein sen omista lähtökohdista käsin. Toisaalta reduktionistista käsitystä ei voida esittää kykenemättömäksi antamaan nopeudelle ulkoista hedelmällistä kykyä toimia selitysvälineenä kappaleen tuleville paikoille, koska tämä kyky ei kuulu käsitykselle alunperinkään, eikä sen mekaniikan selityksiä tarkemmin tarkastellessa tulisikaan. Näin ollen olisi hyvä syy hyväksyä reduktionistinen käsitys nopeuden metafyysiseksi näkemykseksi.

Nopeus toimii eräänlaisena kappaleen liikkeen rajoittajana, joka sillä on liikkuessaan tiettyä rataa tietyssä ajassa tai hetkellisesti. Karkeasti voisi esittää, että kappaleen nopeus ilmaisee miten (tiettyä rataa) liikutaan, mutta ei minne tullaan liikkumaan. Kappaleen nopeus ei voi kausaalisesti määrittää kappaleen tulevia paikkoja. Ei-reduktionistit, kuten Mark Lange ^[8], väittävät puolestaan, että kappaleen nopeus ei määräydy kappaleen radan perusteella ja että kappaleen nopeus vaikuttaa sen tuleviin paikkoihin. Easwaran ^[9] esittää, että tietyt kappaleen paikat määrittävät sen nopeuden, joka kausaalisesti vaikuttaa sen tuleviin paikkoihin. Easwaranin artikkeli Why Physics Use Second Derivatives toimiikin hyvänä jatkolukemisena tälle artikkelille.

Lähteet

Carroll, John W. (2002): ”Instantaneous motion”. Philosophical Studies 110 (1):49 – 67.

Easwaran, Kenny (2014): “Why Physics Uses Second Derivatives”. British Journal for the Philosophy of Science 65 (4):845-862.

Lange, M. (2005): ‘How Can Instantaneous Velocity Fulfill Its Causal Role?’, Philosophical Review, 114, pp. 433–468.

Tooley, M. (1988): ‘In Defense of the Existence of States of Motion’, Philosophical Topics 16, 225–254.

Ulrich, Meyer (2003): “The metaphysics of velocity”. Philosophical Studies 112 (1):93 – 102.

Viitteet